现代计算机存储和处理的信息以二值信号表示,称为位(bit)。将位组合在一起,再加上某种解释(interpretation),我们就能够表示任何有限集合的元素。例如:无符号(unsigned)、补码(two`s-complement)、浮点数(floating-point)。计算机表示法是用有限数量的位来对一个数字编码,因此,结果太大以致不能表示时,某些运算就会溢出(overflow)。溢出会导致某些令人吃惊的后果。
2.1 信息存储
大多数计算机都使用8位的块或者字节(byte)作为最小的可寻址存储单位。
储存器的每个字节都有唯一的一个数字来表示,称为地址(address)。
所有地址集合称为虚拟存储器(virtual address space),实际的实现是随机访问存储器(RAM)、磁盘存储器、特殊硬件喝操作系统软件结合起来,为程序提供的一个看上去统一的字节数组。
2.1.1 十六进制表示法
如果以16为基数表示数字的方法叫做十六进制法(hexadecimal)简写为(hex)。
一个字节的二进制表示 000000002 ~ 111111112;四个二进制位可以缩减成一个十六进制位,这样一个字节就能表示成0016~FF16。C语言中以0x或0X开头的数字常量被认为是十六进制的数值。
| 十六进制数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 十进制数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 二进制数 | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
| 十六进制数 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 十进制数 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 二进制数 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
2.1.2 字
字长(word size)指明整数和指针数据的标称大小(nominal size)。
字长决定的最重要的系统参数就是虚拟地址空间的最大大小。对于一个字长为w位的机器而言,虚拟地址范围是0~2w-1。今天大多数计算机字长都是32位,这就限定了地址空间为4千兆字节(4GB)。
2.1.3 数据大小
| C声明 | 32位机器 | 64位机器 |
| char | 1 | 1 |
| short int | 2 | 2 |
| int | 4 | 4 |
| long int | 4 | 8 |
| long long int | 8 | 8 |
| char * | 4 | 8 |
| float | 4 | 4 |
| double | 8 | 8 |
2.1.4 寻址和字节顺序
最低有效字节在最前面的方式,称为小端法(little endian)。
最高有效字节在最前面的方式,称为大端法(big endian)。
大多数IBM和Sun Microsystems的机器都采用这种规则。
许多比较新的微处理器使用双端法(bi-endian),也就是可以把它们配置成作为大端或者小端的机器运行。
2.1.5 表示字符串
C语言中字符串被编码为一个以null(值为0)字符结尾的字符数组。常用ASCII字符码。
在使用ASCII编码作为字符编码的任何系统上都将得到相同结果,与字节顺序和字大小无关。因此文本数据比二进制数据具有更强的平台独立性。
2.1.6 表示代码
不同机器来行使用不同的指令和编码方式。所以一样的进程运行在不同的操作系统上也会有不同的编码规则。因此二进制代码是不兼容的。二进制代码很少能在不同机器和操作系统中组合之间移植。
2.1.7 布尔代数简介
将逻辑值TRUE(真)和FALSE(假)编码为二进制1和0,能够设计出一种代数,以研究逻辑推理的基本原则。
应用:表示有限集合。比如A={0,3,5,6} 可以表示为a=[01101001];B={0,2,4,6} 表示为 b=[01010101]。然后可以用过位运算来获得A∪B(a^b),A∩B(a&b)。
2.1.8 C语言中的位级运算
C语言所使用的:|(OR),&(AND),~(NOT),^(EXCLUSIVE-OR)。
2.1.9 C语言中的逻辑运算
C语言所使用的:||、&&和!。分别对应命题逻辑中的OR、AND和NOT。
2.1.10 C语言中的位移运算
C语言所使用的:<<(左移)、>>(算术右移:高位补符号位)、>>>(逻辑右移:高位补0)。
实际上,几乎所有的编译器/及其组合都对有符号数据使用算术右移,且许多程序员也会假设机器会使用这种右移。
移动k位,这里k很大
对于一个w位组成的数据类型,如果移动k位,k>=w时,移位指令只会考虑log2w位,因此就相当于移动了k mod w位。
优先级:C语言中移位操作符的优先级低于加减法,因此运算中需要添加括号。
2.2 整数表示
2.2.1 整型数据类型
不同机器的整型数据取值范围会有所不同:
| C数据类型 | 最小值 | 最大值 |
| char | -128 | 127 |
| unsigned char | 0 | 255 |
| short [int] | -32 768 | 32 767 |
| unsigned short [int] | 0 | 65 535 |
| int | -2 147 483 648 | 2 147 483 647 |
| unsigned [int] | 0 | 4 294 967 295 |
| long [int] | -2 147 483 648 | 2 147 483 647 |
| unsigned long [int] | 0 | 4 294 967 295 |
| long long [int] | -9 223 372 036 854 775 808 | 9 223 372 036 854 775 807 |
| unsigned long long [int] | 0 | 18 446 744 073 709 551 615 |
| C数据类型 | 最小值 | 最大值 |
| char | -128 | 127 |
| unsigned char | 0 | 255 |
| short [int] | -32 768 | 32 767 |
| unsigned short [int] | 0 | 65 535 |
| int | -2 147 483 648 | 2 147 483 647 |
| unsigned [int] | 0 | 4 294 967 295 |
| long [int] | -9 223 372 036 854 775 808 | 9 223 372 036 854 775 807 |
| unsigned long [int] | 0 | 18 446 744 073 709 551 615 |
| long long [int] | -9 223 372 036 854 775 808 | 9 223 372 036 854 775 807 |
| unsigned long long [int] | 0 | 18 446 744 073 709 551 615 |
| C数据类型 | 最小值 | 最大值 |
| char | -127 | 127 |
| unsigned char | 0 | 255 |
| short [int] | -32 767 | 32 767 |
| unsigned short [int] | 0 | 65 535 |
| int | -32 767 | 32 767 |
| unsigned [int] | 0 | 65 535 |
| long [int] | -2 147 483 647 | 2 147 483 647 |
| unsigned long [int] | 0 | 4 294 967 295 |
| long long [int] | -9 223 372 036 854 775 807 | 9 223 372 036 854 775 807 |
| unsigned long long [int] | 0 | 18 446 744 073 709 551 615 |
注:C语言标准要求这些数据类型至少有这样的取值范围。
2.2.2 无符号数的编码
假设一个数有$w$位,用$\vec x$表示x的向量,或者写成$[x_{w-1},x_{w-2},\cdots,x_0]$。
$$B2U_w(\vec x)=\displaystyle\sum_{i=0}^{w-1}x_i2^i$$
B2U取值范围$(0 \leq B2U \leq 2^w-1)$
2.2.3 补码编码
如果要表示负值,最常用的表示方式就是补码(two`s-complement)。
$$B2T_w(\vec x)=-x_{w-1}2^{w-1}+\displaystyle\sum^{w-2}_{i=0}x_i2^i$$
B2T取值范围$(-2^{w-1} \leq B2T \leq 2^{w-1}-1)$
2.2.4 有符号数和无符号数之间的转换
对大多数C语言的规则是:数值可能会改变,但是位模式不变。
$$U2T_w(u)=B2T_w(U2B_w(u))=-u_{w-1}2^w+u$$
$$U2T_w(u)=\begin{cases}u,&u<2^w-1\\[2ex]u-2^w,&u\geq2^w-1\\[2ex]\end{cases}$$
$$T2U_w(x)=B2U_w(T2B_w(x))=x_{w-1}2^w+x$$
$$T2U_w(x)=\begin{cases}x+2^w,&x<0\\[2ex]x,&x\geq0\\[2ex]\end{cases}$$
有符号和无符号数之间的转换:$0$~$2^{w-1}-1$不变,$2^{w-1}$~$2^w-1$映射到$-2^w-1$~$-1$。
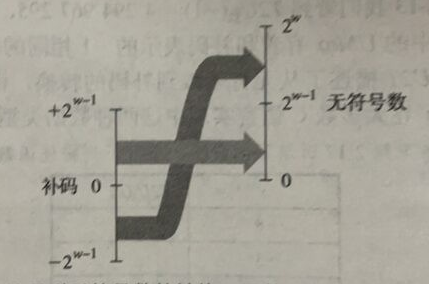
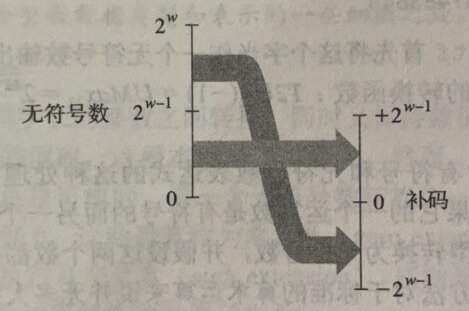
2.2.5 C语言中的有符号数与无符号数
如果一个表达式同时包含有符号数和无符号数,那么C语言会隐式的将有符号数强制转换成无符号数,并假设这两个数都是非负的。这样会出现一些奇特的现象:
| 表达式 | 类型 | 求值 |
| 0 == 0U | 无符号 | 1 |
| -1 < 0 | 有符号 | 1 |
| -1 < 0U | 无符号 | 0* |
| 2147483647 > -2147483647-11 | 有符号 | 1 |
| 2147483647U > -2147483647-1 | 无符号 | 0* |
| 2147483647 > (int)-2147483648U | 有符号 | 1* |
| -1 > -2 | 有符号 | 1 |
| (unsigned) -1 > -2 | 无符号 | 1 |
2.2.6 扩展一个数字的位表示
- 零扩展(zero extension):添加0。
- 符号扩展(sign extension):添加最高有效位值的副本。
2.2.7 截断数字
丢弃高位数字,符号位也会被丢弃。
2.2.8 关于有符号数与无符号数的建议
为避免转换出现的奇特现象,一种方法就是绝不使用无符号数。必如Java只支持有符号数,并要求用补码来实现。
2.3 整数运算
理解计算机运算的细微之处有助于程序员编写更可靠的代码。比如为什么两个正数相加会产生一个负数。
2.3.1 无符号加法
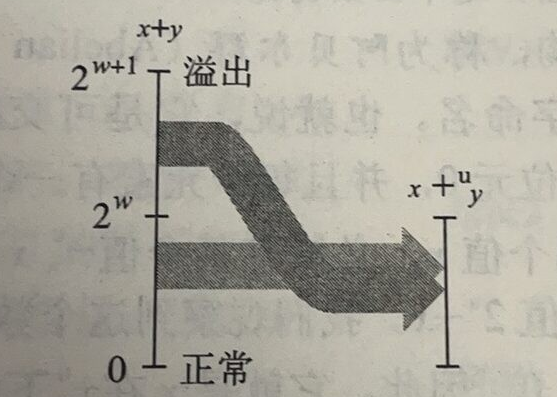
如果两个无符号数相加之和产生了溢出(overflow),那么会截断数字:
$$x+^u_wy=\begin{cases}x+y, &x+y<2^w\\[2ex]x+y-2^w, &2^w \leq x+y < 2^{w+1}\\[2ex]\end{cases}$$
$$-^u_wx=\begin{cases}x, &x = 0\\[2ex]2^w-x, &x > 0\\[2ex]\end{cases}$$
2.3.2 补码加法
$$\begin{align}x+^t_wy & =U2T_w(T2U_w(x)+^u_wT2U_w(y))\\ & =U2T_w[(x+y) mod 2^w] \end{align}$$
$$x+^t_wy=\begin{cases}x+y-2^w,&2^{w-1}\le x+y&\text{正溢出}\\[2ex]x+y,&-2^{w-1}\le x+y<2^{w-1}&\text{正常}\\[2ex]x+y+2^w,&x+y<-2^{w-1}&\text{负溢出}\\[2ex]\end{cases}$$

2.3.3 补码的非
$$-^t_wx=\begin{cases}-2^{w-1},&x=-2^{w-1}\\[2ex]-x,&x>-2^{w-1}\\[2ex]\end{cases}$$
2.3.4 无符号乘法
$$x *^u_w y = (x \cdot y) mod 2^w$$
无符号乘积进行截断
2.3.5 补码乘法
同无符号乘法,w位数字上的无符号运算和补码运算时同构的。
2.3.6 乘以常数
编译器会尝试使用位移和加法来代替乘以常数因子的乘法。
2.3.7 除以2的幂
使用右移实现。
2.3.8 关于整数运算的最后思考
- 计算机的整数运算,实际上是一种模运算形式
- 补码是一种灵活的表示方法,可以表示正数和负数,而且执行算数的位级实现(加、减、乘、除)都和无符号形式一致。
- C语言某些规定会导致一些特别的结果,特别是unsigned数据类型。
2.4 浮点数
所有的计算机都支持IEEE(读作 Eye-Triple-Eee)浮点标准。当一个数字不能准确表示的时候会使用舍入(rounding)来近似表示。
2.4.1 二进制小数
通过十进制小数的数学表述:
$$d = \displaystyle\sum_{i=-n}^m 10^i \times d_i$$
同理转化成二进制表示:
$$b = \displaystyle\sum_{i=-n}^m 2^i \times b_i$$
2.4.2 IEEE浮点表示
IEEE浮点标准用$V=(-1)^s \times M \times 2^E$的形式来表示一个数:
- s:符号(sign)
- M:尾数(significand)
- E:阶码(exponent)
常用的浮点数的表示,分为三个部分:s(符号位)、k(阶码)、n(尾数)。
- 单精度(32位):$[s_0,k_7,\cdots,k_0,n_{22},\cdots,n_1,n_0]$
- 双精度(64位):$[s_0,k_{10},\cdots,k_0,n_{51},\cdots,n_1,n_0]$
- $[n_{31},\cdots,n_1,n_0]$
根据阶码的值,被编码的值可以分成三种不同的情况。
- 情况一:规格化的值
阶码的二进制表示不全为0,也不全为1时。偏置(biased)是阶码的表示方法,也叫做移码。
$$E=e-\text{Bias}$$
e就是阶码的无符号值,Bias值为$2^{k-1}-1$;尾数的取值为$M=1+\vec n$。其中$0 \le \vec n < 1$,这种方式也叫做隐含的以1开头的(implied leading 1)表示。这样我们使得尾数M的范围在[1 , 2)之间。由于第一位总是等于1,这样就能额外获得一个精度位,因此我们就不需要显示的表示它。 - 情况二:非规格化的值
当阶码全为0时,阶码值是$E=1-Bias$(这样让数值有了一个平滑的过渡),尾数值是$\vec n$,不包含隐含的开头1。
非规格数的作用有两个:1)表示0 2)表示接近0的数。 - 情况三:
当阶码全为1时出现。根据尾数的不同有三种数值:
1)当尾数全为0时, 值为$+\infty$
2)当尾数全为1时, 值为$-\infty$
3)其余情况, 值为NaN(Not a Number)
2.4.3 数字示例
六位数的数值分布:

八位浮点格式的非负值示例:
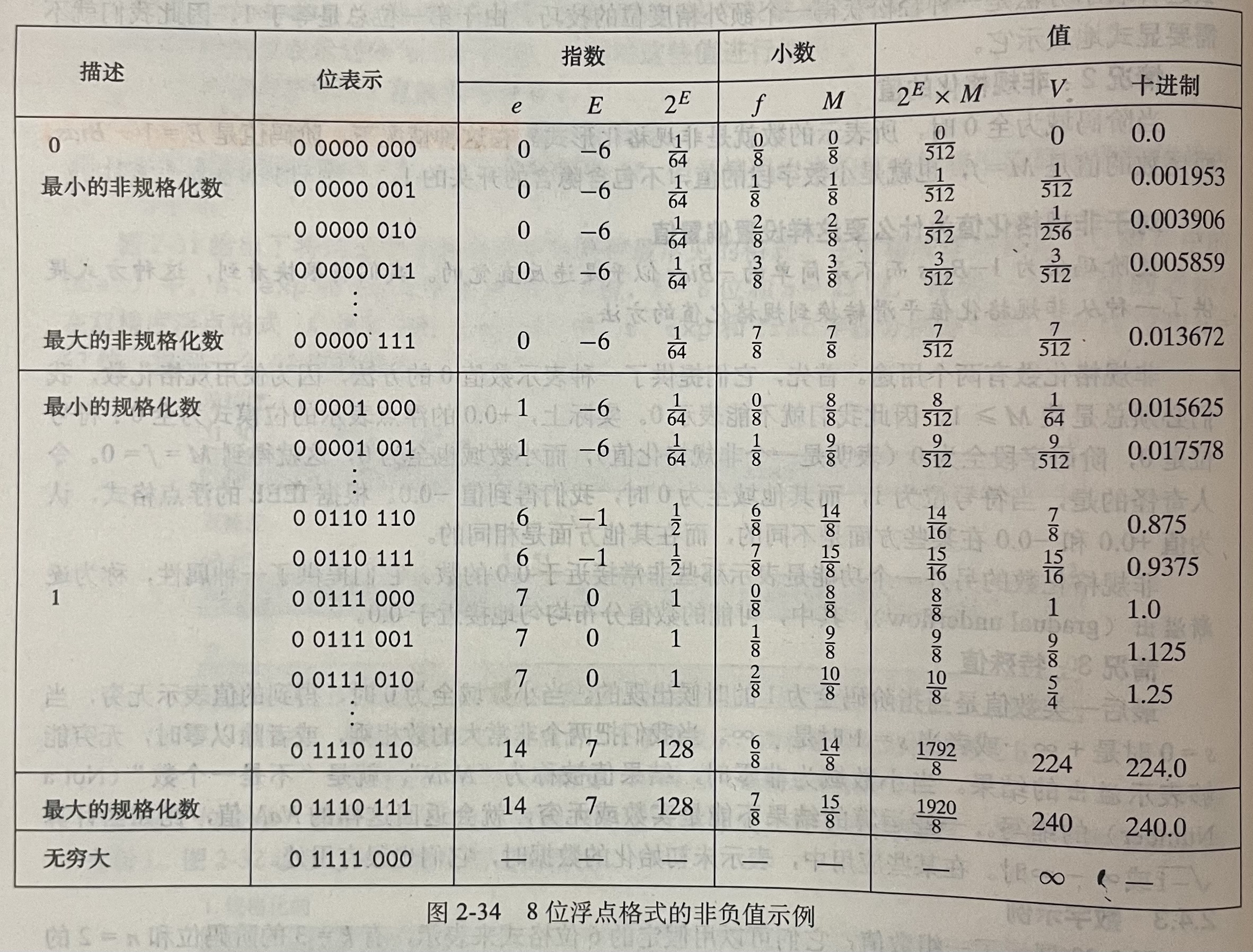
IEEE的设计时为了浮点数能够使用整数排序函数来进行排序。
2.4.4 舍入
舍入(rounding):通过运算,将一个超出浮点数范围和精度的数,匹配到”最接近的“值上。
四种舍入方式:
- 向偶数舍入(round-to-nearest):这是默认的方式。舍入之后的最低为为偶数。如果1.5和2.5进行四舍五入然后求平均值,这种方式无疑会更加准确。同时偶数舍入法可以在二进制数中使用:$X\cdots X.Y\cdots Y100\cdots$2表示要舍入到最右边一个Y的位,这种情况下如果Y是0就会直接截去之后的数,如果Y是1就会加上1并向上进位。
- 向零舍入:正负值都向原点舍入,比如Round(1.5)=1,Round(-1.5)=-1。
- 向下舍入:正负值都向更小的整数舍入,比如Round(1.5)=1,Round(-1.5)=-2。
- 向上舍入:正负值都向更大的整数舍入,比如Round(1.5)=2,Round(-1.5)=-1。
2.4.5 浮点运算
浮点运算相较于整数运算,会丧失一些特性,但是会比整数运算多一些实数的特性。
比如:浮点运算不具备结核性,和分配性。因为不同的运算顺序会因为精度的损失导致结果的不同,所以计算机在保守的前提下不会优化这类代码。
又如:浮点运算满足了单调性即如果$a \ge b$,那么对于任何$a,b,x$,除了NaN,都有$x+a \ge x+b$。整数运算则可能会溢出。
2.5 小结
- 不同的编码表示不同的信息时,计算机会使用不同的约定。
- C语言有多种数值的实现,理解他们的差异很重要。
- C语言隐式类型转换会出现无法预测的结果。
- C语言实现的整数运算和真是的整数运算相比有一些特殊的属性,例如:溢出
- 位级运算和算术运算的组合有助于更方便的解决一些问题。例如:补码运算~x+1等价于-x;用位向量运算掩码。
- 理解浮点数的表示,通常是由IEEE标准754定义的。
- DATA:TMIN C语言中TMin的写法:TMin32写成-2147483647-1,原因是C语言补码表示的不对称性和奇怪的转换方式迫使我们不得不用这种不同寻常的方式来写。 ↩︎
- 比如要舍入到最近的$2^{-2}$位置时:$10.00011_2(2\frac {3}{32})$向下舍入到$10.00_2(2)$,$10.00110_2(2\frac {3}{16})$向上舍入到$10.01_2(2\frac {1}{4})$,$1011100_2(2\frac {7}{8})$向上舍入到$11.00_2(3)$,而$10.10100_2(2\frac {5}{8})$向下舍入到$10.10_2(2\frac {1}{2})$。 ↩︎
